Lagrange Points
The point near two large bodies in orbit such that if a third body (of negligible mass) is placed at that point, it will remain stationary with respect to the two large bodies is called a Lagrange point.
Derivation
Assume two bodies of masses \(m_1\) and \(m_2\) are in circular orbits around their center of mass (placed at the origin), with the same angular velocity, \(\omega\). Without loss of generality, let’s further assume that the two bodies are in the XY-plane.
Using the law of gravitation, we can find out the distances of these two bodies from their center of mass (i.e. the origin). Let’s assume that the distance of the first body from the origin is \(r_1\) (i.e. placed at \((-r_1, 0, 0)\)) and the distance of the second body from the origin is \(r_2\) (i.e. placed at \((r_2, 0, 0)\)). Hence, we get:
\[\begin{equation} m_1r_1 = m_2r_2 \end{equation}\]We can very easily calculate the orbital speed \(\omega\) from this:
\[\begin{equation} \begin{split} \frac{Gm_1m_2}{(r_1+r_2)^2} &= m_1 \omega^2 r_1 \\ \frac{Gm_1m_2}{(r_1+r_2)^2} &= m_2 \omega^2 r_2 \end{split} \end{equation}\]Hence, we get,
\[\begin{equation} \begin{split} Gm_1 &= r_2 (r_1+r_2)^2 \omega^2 \\ Gm_1 &= r_2 (r_1+r_2)^2 \omega^2 \\ \Rightarrow G(m_1+m_2) &= (r_1+r_2)^3 \omega^2 \\ \Rightarrow \omega &= \sqrt{\frac{G(m_1+m_2)}{(r_1+r_2)^3}} \end{split} \end{equation}\]Now, let’s introduce a third body in this two body system of mass \(m_3 (\ll m_1, m_2)\) at \((x, y, z)\). For this body to be at a lagrange point, it must, by definition, remain stationary w.r.t. \(m_1\) and \(m_2\). That is, it must also orbit the origin with only an angular speed \(\omega\) along the Z-axis.
Before we start calculating the gravitational forces on \(m_3\), we need to keep in mind that if it is located at \(z \neq 0\), it will always experience a force towards the XY-plane due to the presence of \(m_1\) and \(m_2\) in the XY-plane. Hence, \(a_z\) (acceleration in the z-direction) will never be equal to 0, thereby failing to be at a lagrange point. So, there exist no lagrange points having \(z \neq 0\). Consequently, we shall restrict ourselves to finding point(s) in the XY-plane only and will be of the form \((x, y, 0)\).
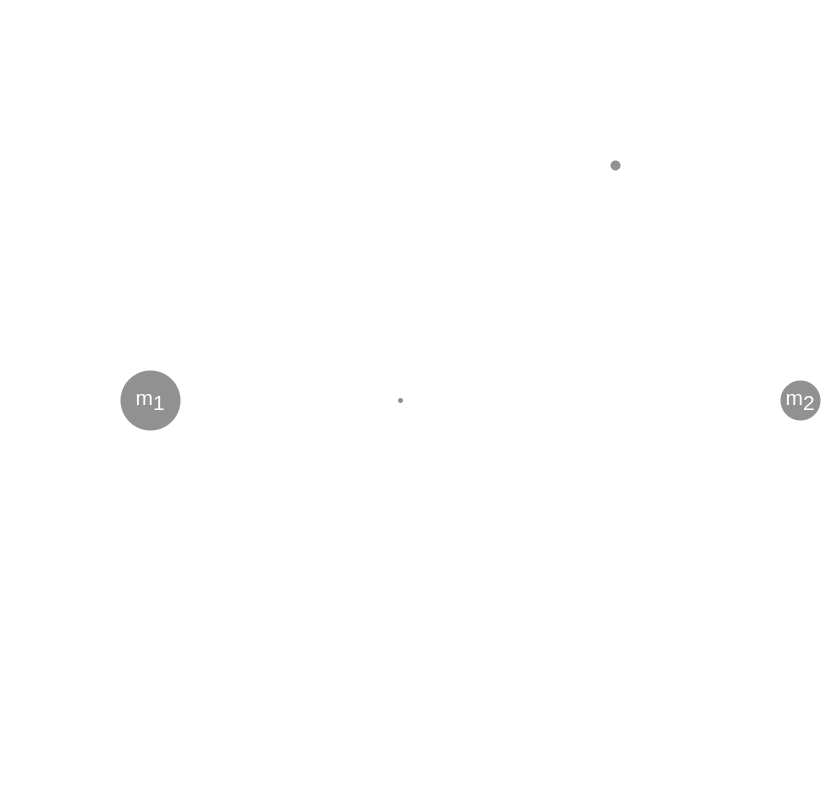
Coming back to calculating the gravitational forces acting on \(m_3\), the gravitational force acting on \(m_3\) due to \(m_1\) can be given as:
\[\begin{equation} \begin{split} \vec{F_1} &= -\frac{Gm_1m_3}{r_{31}^2}\hat{r_{31}} \\ &= -\frac{Gm_1m_3}{((x+r_1)^2 + y^2)^{3/2}} ((x+r_1)\hat{i} + y\hat{j}) \end{split} \end{equation}\]Similarly, the gravitational force acting on \(m_3\) due to \(m_2\) can be written as:
\[\begin{equation} \begin{split} \vec{F_2} &= -\frac{Gm_2m_3}{r_{32}^2}\hat{r_{32}} \\ &= -\frac{Gm_2m_3}{((x-r_2)^2 + y^2)^{3/2}} ((x-r_2)\hat{i} + y\hat{j}) \end{split} \end{equation}\]The sum of these two forces should be equal to the centripetal force required by \(m_3\) to orbit the origin with an angular velocity of \(\omega\) about the Z-axis. Mathematically,
\[\begin{equation} \vec{F_1} + \vec{F_2} = -m_3 \omega^2 (x\hat{i} + y\hat{j}) \end{equation}\]Separating the force balance equation into its components along the X- and Y-axis, we get,
\[\begin{equation} \begin{split} m_3 \omega^2 x &= \frac{Gm_1m_3}{((x+r_1)^2 + y^2)^{3/2}} (x+r_1) + \frac{Gm_2m_3}{((x-r_2)^2 + y^2)^{3/2}} (x-r_2) \\ m_3 \omega^2 y &= \frac{Gm_1m_3}{((x+r_1)^2 + y^2)^{3/2}} y + \frac{Gm_2m_3}{((x-r_2)^2 + y^2)^{3/2}} y \end{split} \end{equation}\]Easy solution(s) of this can be obtained by finding lagrange point(s) on the X-axis, i.e., by taking \(y = 0\). This reduces the above equations to:
\[\begin{equation} \begin{split} m_3 \omega^2 x &= \frac{Gm_1m_3}{(x+r_1)^2} + \frac{Gm_2m_3}{(x-r_2)^2} \\ 0 &= 0 \\ \end{split} \end{equation}\]Substituting the value of \(\omega\), we end up with a third order polynomial in \(x\), i.e., a cubic equation. It will have three roots, denoting three lagrange points, namely, \(L1\), \(L2\) and \(L3\). The calculation of the exact values of these are left as an exercise to the you :p
These three lagrange points will always be found in the following three regions:
- Before \(x = -r_1\)
- Between \(x = -r_1\) and \(x = r_2\)
- Beyond \(x = r_2\)
And will, as proven above, have \(y = 0\) and \(z = 0\)
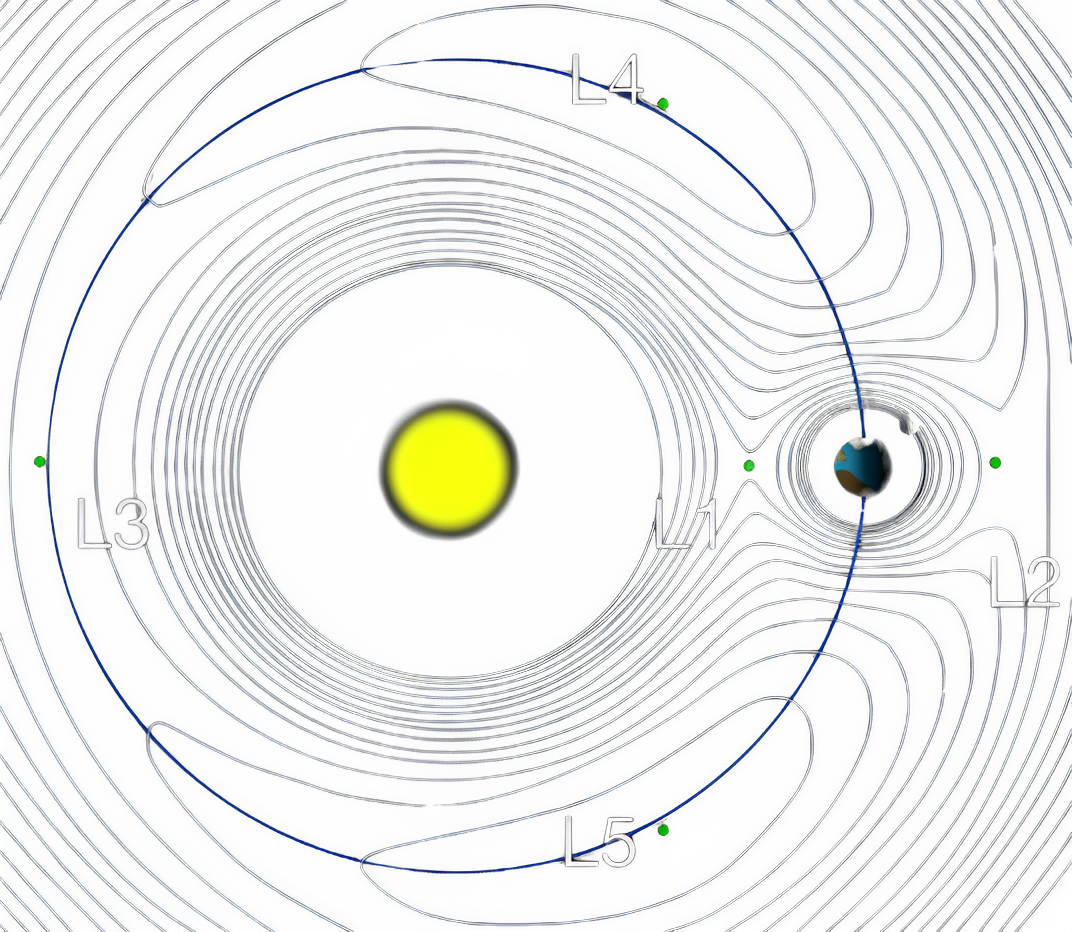
Now, if we take \(y \neq 0\), we get 2 solutions, giving us two more lagrange points, namely, \(L4\) and \(L5\).
Connect a line segment from \(m_1\) to \(m_2\) and using this length, draw two equilateral triangles on the XY-plane with this line segment as one of the edges. The third vertex of these triangles will be the \(L4\) and \(L5\) lagrange points.
Hence, they are also known as equilateral lagrange points
Stability
The stability of a lagrange point is defined by its ability to retain the object at that point if slight perturbation is introduced in the position of \(m_3\). If \(m_3\) returns back to the same lagrange point, that lagrange point is considered to be stable. It is declared unstable otherwise.
In orbiting two-body systems, the lagrange points \(L_1\), \(L_2\) and \(L_3\) are unstable and the lagrange points \(L_4\) and \(L_5\) are stable as can be seen in the image below (Credits: wordpress.mrreid.org)
Utility
Lagrange points offer a lot of advantages. A few of them include:
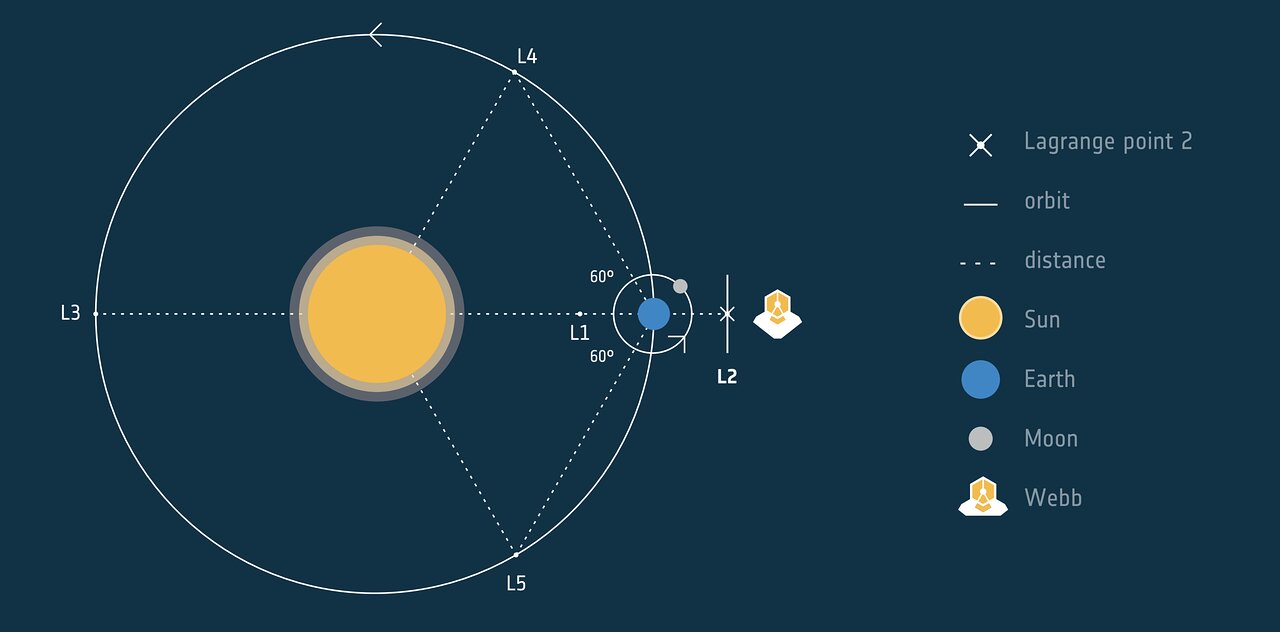
- Placement of telescopes near \(L1\) and \(L2\). \(L1\) is an absolutely brilliant point for placement of solar observatories as they’ll be able to get un-blocked view of the Sun 24x7. Examples include the Aditya L1 mission. Similarly, \(L2\) is an ideal location for an infrared observatory, for example, the James Webb Space Telescope. (Image credits: ESA Webb)
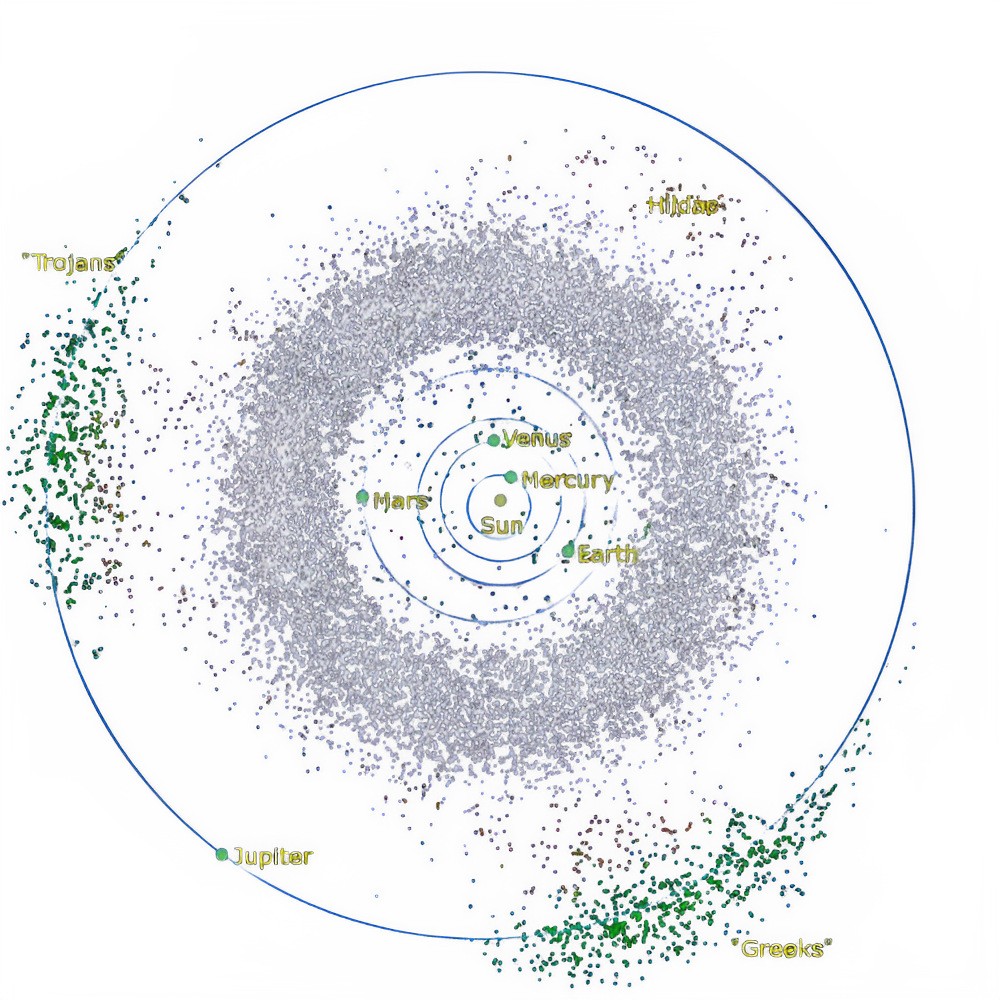
- Protection from rouge asteroids and comets. A massive planet, such as Jupiter, captures and holds potentially devastating asteroids and comets that may come towards the inner planets (such as the Earth), near its lagrange points, particulartly the stable \(L4\) and \(L5\) lagrange points. (Image credits: Mdf)
These are called Trojan asteroids, which are named after characters from Homer’s lliad (the legendary siege of Troy).
Asteroids at the \(L4\) points, which leads Jupiter, are referred to as the “Greek camp”, while at the \(L5\) points are referred to as the “Trojan camp”. These asteroids are largely named after characters from the respective sides of the Trojan war.